Einführung
- 4178
- 1221
- Matteo Möllinger
In diesem schnellen GNU -Tutorial für statistische Modelle und Grafiken bieten wir ein einfaches Beispiel für lineare Regressionen und lernen, wie man eine solche grundlegende statistische Analyse von Daten ausführt. Diese Analyse wird von grafischen Beispielen begleitet, die uns dem Erstellen von Diagrammen und Diagrammen mit GNU R näher bringen werden. Wenn Sie mit R überhaupt nicht vertraut sind.
Modelle und Formeln in r
Wir verstehen a Modell in Statistiken als präzise Beschreibung der Daten. Eine solche Präsentation von Daten wird normalerweise mit a gezeigt mathematische Formel. R hat seinen eigenen Weg, um Beziehungen zwischen Variablen darzustellen. Zum Beispiel die folgende Beziehung y = c0+C1X1+C2X2+… +CNXN+r ist in r geschrieben als
y ~ x1+x2+…+xn,
Das ist ein Formelobjekt.
Beispiel für lineare Regression
Lassen Sie uns nun ein lineares Regressionsbeispiel für GNU R angeben, das aus zwei Teilen besteht. Im ersten Teil dieser Beispiel. Zusätzlich fügen wir im zweiten Teil des Beispiels unserer Analyse eine weitere Variable hinzu, die die auf Euro bezeichneten Index zurücksetzt.
Einfache lineare Regression
Laden Sie die Beispieldatendatei in Ihr Arbeitsverzeichnis herunter: Regression-Example-Gnu-r.CSV
Lassen Sie uns nun R in Linux vom Ort des Arbeitsverzeichnisses einfach durchführen
$ R
und lesen Sie die Daten aus unserer Beispieldatendatei:
> Gibt zurück<-read.csv("regression-example-gnu-r.csv",header=TRUE) Sie können die Namen der Variablen eintippen sehen
> Namen (zurückgegeben)
[1] "USA" "Kanada" "Deutschland"
Es ist Zeit, unser statistisches Modell zu definieren und eine lineare Regression durchzuführen. Dies kann in den folgenden wenigen Codezeilen erfolgen:
> y<-returns[,1]
> x1<-returns[,2]
> Gibt zurück.lm<-lm(formula=y~x1)
Um die Zusammenfassung der Regressionsanalyse anzuzeigen, führen wir die aus Zusammenfassung() Funktion auf dem zurückgegebenen Objekt kehrt zurück.lm. Das ist,
> Zusammenfassung (Rückgabe.lm)
Forderung:
LM (Formel = y ~ x1)
Residuen:
Min 1Q Median 3q Max
-0.038044 -0.001622 0.000001 0.001631 0.050251
Koeffizienten:
Schätzung std. Fehler t Wert PR (> | T |)
(Abfang) 3.174e-05 3.862e-05 0.822 0.411
x1 9.275e-01 4.880E-03 190.062 <2e-16 ***
---
Signifikant. Codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.'0.1 "1
Reststandardfehler: 0.003921 auf 10332 Freiheitsgrade
Mehrfach R-Quadrat: 0.7776, angepasstes R-Quadrat: 0.7776
F-Statistik: 3.612e+04 auf 1 und 10332 df, p-Wert: < 2.2e-16
Diese Funktion gibt das obige entsprechende Ergebnis aus. Die geschätzten Koeffizienten sind hier c0~ 3.174e-05 und c1 ~ 9.275E-01. Die obigen P-Werte legen nahe, dass der geschätzte Abfang C0 unterscheidet sich nicht wesentlich von Null, daher kann es vernachlässigt werden. Der zweite Koeffizient unterscheidet sich signifikant von Null seit dem P-Wert<2e-16. Therefore, our estimated model is represented by: y=0.93 x1. Darüber hinaus ist R-Quadrat 0.78, was bedeutet, dass etwa 78% der Varianz in der Variablen y durch das Modell erklärt werden.
Mehrere lineare Regression
Fügen wir nun unser Modell eine weitere Variable hinzu und führen wir eine multiple Regressionsanalyse durch. Die Frage ist nun, ob das Hinzufügen einer weiteren Variablen zu unserem Modell ein zuverlässigeres Modell erzeugt.
> x2<-returns[,3]
> Gibt zurück.lm<-lm(formula=y~x1+x2)
> Zusammenfassung (Rückgabe.lm)
Forderung:
LM (Formel = y ~ x1 + x2)
Residuen:
Min 1Q Median 3q Max
-0.0244426 -0.0016599 0.0000053 0.0016889 0.0259443
Koeffizienten:
Schätzung std. Fehler t Wert PR (> | T |)
(Abfang) 2.385e-05 3.035e-05 0.786 0.432
x1 6.736e-01 4.978e-03 135.307 <2e-16 ***
x2 3.026e-01 3.783E-03 80.001 <2e-16 ***
---
Signifikant. Codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.'0.1 "1
Reststandardfehler: 0.003081 auf 10331 Freiheitsgraden
Mehrfach R-Quadrat: 0.8627, angepasstes R-Quadrat: 0.8626
F-Statistik: 3.245E+04 auf 2 und 10331 df, p-Wert: < 2.2e-16
Oben können wir das Ergebnis der multiplen Regressionsanalyse nach Zugabe der Variablen x sehen2. Diese Variable repräsentiert die Renditen des Finanzindex im Euro. Wir erhalten jetzt ein zuverlässigeres Modell, da der angepasste R-Quadrat 0 beträgt.86, was größer ist als der Wert, der vor gleich 0 erhalten wurde.76. Beachten Sie, dass wir das angepasste R-Quadrat verglichen haben, da es die Anzahl der Werte und die Stichprobengröße berücksichtigt. Auch hier ist der Abfangkoeffizient nicht signifikant. Daher kann das geschätzte Modell als: y = 0 dargestellt werden.67x1+0.30x2.
Beachten Sie auch, dass wir beispielsweise unsere Datenvektoren mit ihren Namen hätten verweisen können
> LM (Returns $ USA ~ kehrt $ Canada zurück)
Forderung:
LM (Formel = Rückgabe $ USA ~ Rückgabe $ Canada)
Koeffizienten:
(Abfang) kehrt $ Canada zurück
3.174e-05 9.275E-01
Grafik
In diesem Abschnitt werden wir demonstrieren, wie R für die Visualisierung einiger Eigenschaften in den Daten verwendet wird. Wir werden Abbildungen veranschaulichen, die von Funktionen wie so erhalten wurden wie Parzelle(), Box-Plot(), Hist (), qqnorm ().
Streudiagramm
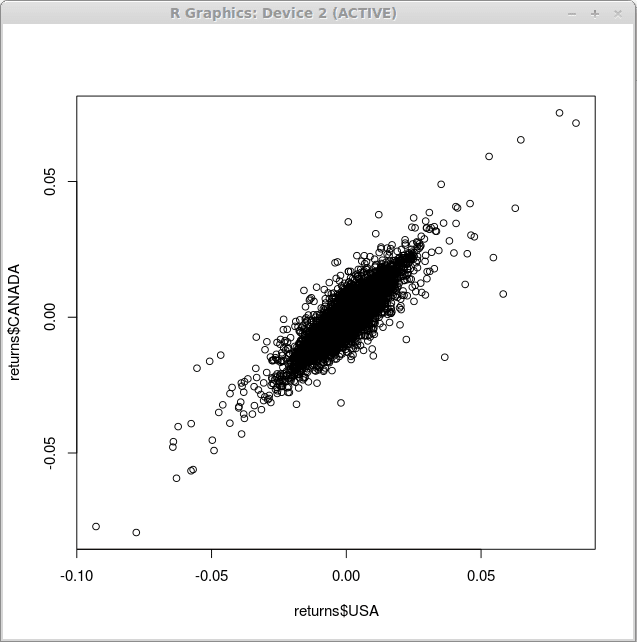
Wahrscheinlich ist die einfachste aller Grafiken, die Sie mit R erhalten können, das Streudiagramm. Um die Beziehung zwischen der US -Dollar -Konfession der Finanzindexrenditen und der kanadischen Dollar -Konfession zu veranschaulichen, verwenden wir die Funktion Parzelle() folgendermaßen:
> Diagramm (Rückgabe $ USA, kehrt $ Canada zurück)
Infolge der Ausführung dieser Funktion erhalten wir ein Streuungsdiagramm, wie unten gezeigt

Eines der wichtigsten Argumente, die Sie an die Funktion übergeben können Parzelle() ist "Typ". Es bestimmt, welche Art von Handlung gezogen werden sollte. Mögliche Typen sind:
• '”P”'Für *p *Salint
• '”l”'Für *l *Ines
• '”B"' für beide
• '”C"" Für die Zeilen Teil allein von "B" ""
• '”Ö"'Für beide'*o*verpielded '
• '”H"'Für'*h*istogramm 'wie (oder" Hochdichte ") vertikale Linien
• '”S„'Für Treppen *s *teps
• '”S„'Für andere Art von *S *teps
• '”N„'Für keine Verschwörung
Um eine Regressionslinie über das obige Streudiagramm zu überlagern, verwenden wir die Kurve() Funktion mit dem Argument 'Add' und 'col', das feststellt.
> Kurve (0.93*x, -0.1,0.1, add = true, col = 2)
Folglich erhalten wir die folgenden Änderungen in unserer Grafik:
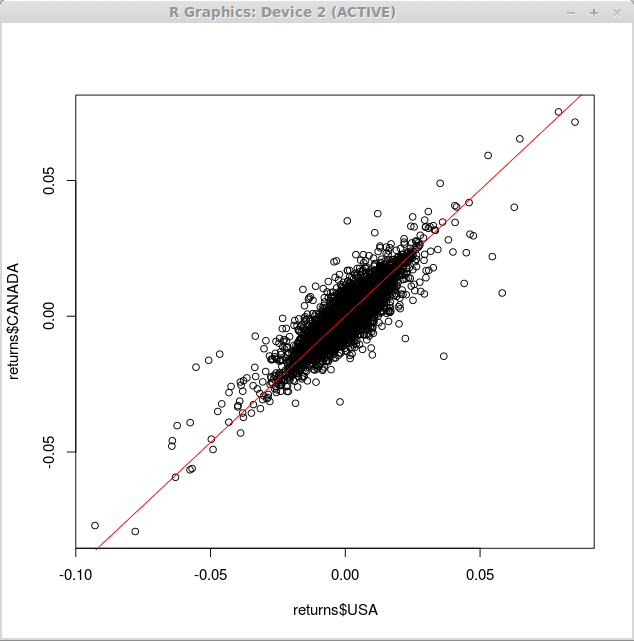
Weitere Informationen zum Funktionsdiagramm () oder Linien () verwenden Sie die Funktion Hilfe(), zum Beispiel
> Hilfe (Handlung)
Box-Plot
Lassen Sie uns nun sehen, wie man das benutzt Box-Plot() Funktion zur Veranschaulichung der Datenbeschreibungsstatistik. Erstellen Sie zunächst eine Zusammenfassung der beschreibenden Statistiken für unsere Daten durch die Zusammenfassung() Funktion und dann die ausführen Box-Plot() Funktion für unsere Rückgaben:
> Zusammenfassung (Rückgabe)
USA Kanada Deutschland
Mindest. : -0.0928805 min. : -0.0792810 min. : -0.0901134
1. Qu.: -0.0036463 1. Qu.: -0.0038282 1. Qu.: -0.0046976
Median: 0.0005977 Median: 0.0005318 Median: 0.0005021
Mittelwert: 0.0003897 Mittelwert: 0.0003859 Mittelwert: 0.0003499
3. Qu.: 0.0046566 3. Qu.: 0.0047591 3. Qu.: 0.0056872
Max. : 0.0852364 Max. : 0.0752731 Max. : 0.0927688
Beachten Sie, dass die deskriptiven Statistiken für alle drei Vektoren ähnlich sind. Daher können wir ähnliche Boxplots für alle Sätze von finanziellen Renditen erwarten. Führen Sie nun die Funktion boxplot () wie folgt aus
> Boxplot (zurückgegeben)
Infolgedessen erhalten wir die folgenden drei Boxplots.
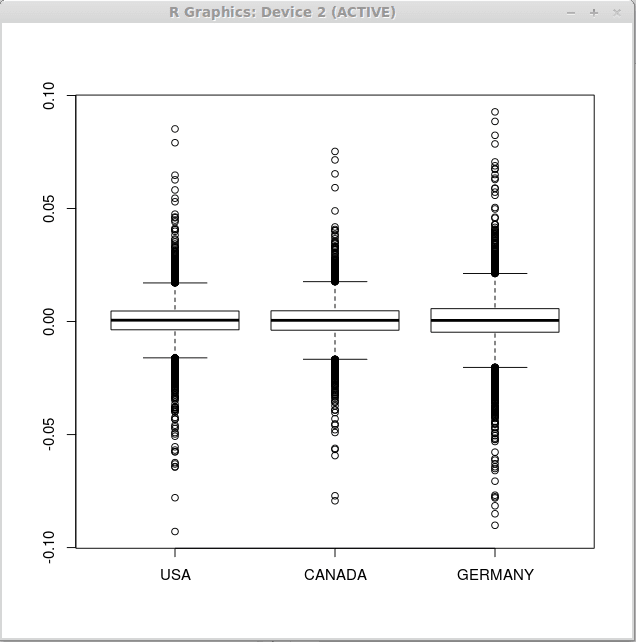
Histogramm
In diesem Abschnitt werden wir uns Histogramme ansehen. Das Frequenzhistogramm wurde bereits in der Einführung in das Gnu R auf Linux -Betriebssystem eingeführt. Wir werden jetzt das Dichtehistogramm für normalisierte Renditen produzieren und es mit der normalen Dichtekurve vergleichen.
Normalisieren wir zunächst die Renditen des in US -Dollars bezeichneten Index, um Null -Mittelwert und Varianz gleich einem zu erhalten, um die realen Daten mit der theoretischen Standard -Normaldichtefunktion vergleichen zu können.
> Retus.Norm<-(returns$USA-mean(returns$USA))/sqrt(var(returns$USA))
> Mean (Retus.Norm)
[1] -1.053152e-17
> var (Retus.Norm)
[1] 1
Jetzt produzieren wir das Dichtehistogramm für solche normalisierten Renditen und zeichnen eine Standard -normale Dichtekurve über ein solches Histogramm auf. Dies kann durch den folgenden R -Ausdruck erreicht werden
> HIST (Retus.Norm, bricht = 50, freq = false)
> Kurve (dnorm (x),-10,10, add = true, col = 2)
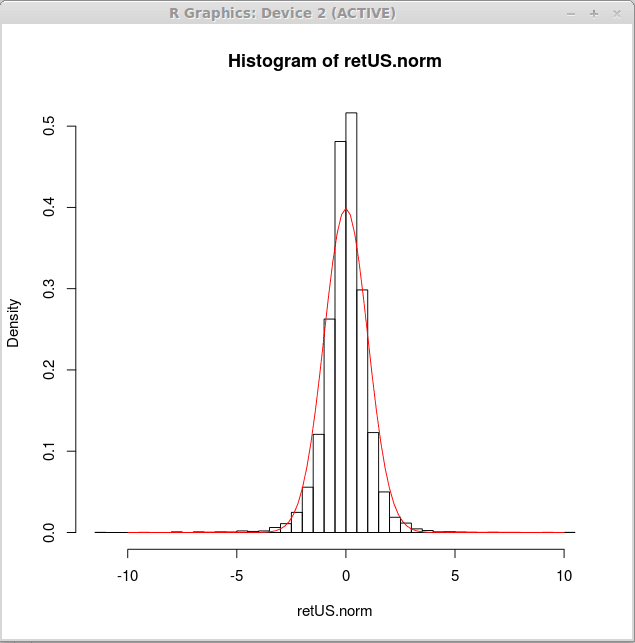
Visuell passt die normale Kurve nicht gut zu den Daten. Eine andere Verteilung kann besser für finanzielle Renditen geeignet sein. Wir werden lernen, wie man eine Verteilung in die Daten in späteren Artikeln passt. Im Moment können wir zu dem Schluss kommen, dass die geeignetere Verteilung in der Mitte mehr ausgewählt wird und schwerere Schwänze haben wird.
QQ-Plot
Ein weiteres nützliches Diagramm in der statistischen Analyse ist der QQ-Plot. Der QQ-Plot ist ein quantiles Quantildiagramm, das die Quantile der empirischen Dichte mit den Quantilen der theoretischen Dichte vergleicht. Wenn diese gut passen, sollten wir eine gerade Linie sehen. Vergleichen wir nun die Verteilung der Residuen, die durch unsere obige Regressionsanalyse erhalten wurden. Zuerst erhalten wir einen QQ-Plot für die einfache lineare Regression und dann für die multiple lineare Regression. Der Typ des von uns verwendeten QQ-Plot ist der normale QQ-Plot, was bedeutet, dass die theoretischen Quantile im Diagramm Quantilen der Normalverteilung entsprechen.
Das erste Diagramm, das den einfachen linearen Regressionsresten entspricht qqnorm () auf die folgende Weise:
> Gibt zurück.lm<-lm(returns$US~returns$CANADA)
> QQNORM (Rückgabe.LM $ Reste)
Das entsprechende Diagramm wird unten angezeigt:
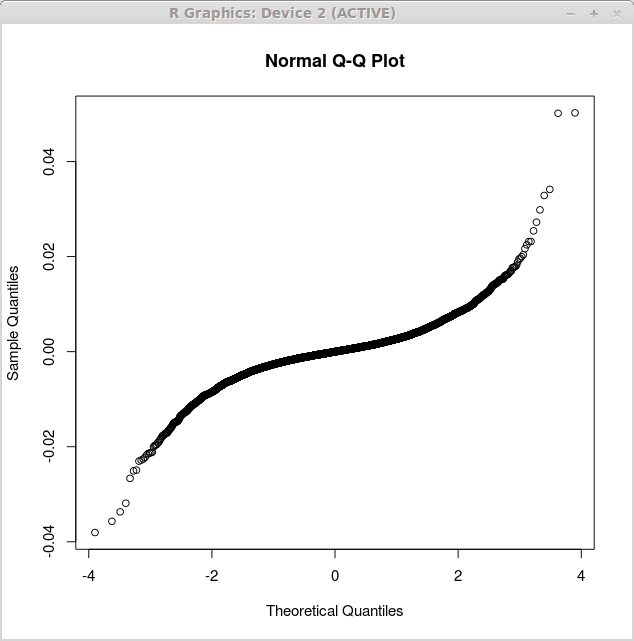
Das zweite Diagramm entspricht den multiplen linearen Regressionsresten und wird als:
> Gibt zurück.lm<-lm(returns$US~returns$CANADA+returns$GERMANY)
> QQNORM (Rückgabe.LM $ Reste)
Dieses Diagramm wird unten angezeigt:
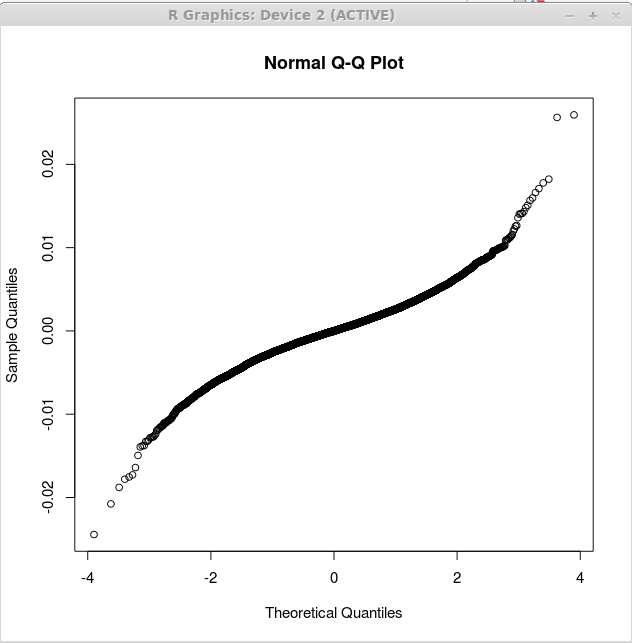
Beachten Sie, dass das zweite Diagramm näher an der geraden Linie liegt. Dies deutet darauf hin, dass die durch die multiplen Regressionsanalyse produzierten Residuen näher an normal verteilten. Dies unterstützt das zweite Modell weiter als nützlicher gegenüber dem ersten Regressionsmodell.
Abschluss
In diesem Artikel haben wir die statistische Modellierung mit GNU R zum Beispiel einer linearen Regression eingeführt. Wir haben auch einige häufig verwendete in Statistikdiagrammen diskutiert. Ich hoffe, dies hat eine Tür zur statistischen Analyse mit Gnu r für Sie geöffnet. Wir werden in späteren Artikeln komplexere Anwendungen von R für die statistische Modellierung sowie die Programmierung diskutieren. Lesen Sie also weiter.
GNU R Tutorial Series:
Teil I: GNU R Einführungs -Tutorials:
- Einführung in GNU R auf Linux -Betriebssystem
- Ausführen von GNU R auf Linux -Betriebssystem
- Ein kurzes GNU -Tutorial für grundlegende Operationen, Funktionen und Datenstrukturen
- Ein kurzes GNU -Tutorial für statistische Modelle und Grafiken
- So installieren und verwenden Sie Pakete in GNU r
- Basis von Grundpaketen in GNU r bauen
Teil II: GNU R -Sprache:
- Ein Überblick über die GNU R -Programmiersprache
Verwandte Linux -Tutorials:
- Eine Einführung in Linux -Automatisierung, Tools und Techniken
- Dinge zu installieren auf Ubuntu 20.04
- Mastering -Bash -Skriptschleifen beherrschen
- Dinge zu tun nach der Installation Ubuntu 20.04 fokale Fossa Linux
- Verschachtelte Schleifen in Bash -Skripten
- Mint 20: Besser als Ubuntu und Microsoft Windows?
- Umgang mit Benutzereingaben in Bash -Skripten
- Ubuntu 20.04 Tricks und Dinge, die Sie vielleicht nicht wissen
- Big Data Manipulation zum Spaß und Gewinn Teil 1
- Ubuntu 20.04 Leitfaden

